我们知道,对于电功率(信号)而言,一般有两种形式:交流和直流。特斯拉推广的是交流电,爱迪生推广的是直流电。两者都各有优点,谁也取代不了谁。在特斯拉和爱迪生的年代,这两者之间是不可调和的,但是随着半导体技术的发展,他们又在某种程度上有一定的缓和,因为是可以相互变换的。具体来说:交流变交流→变压器;交流变直流→整流器;直流变交流→逆变器;直流变直流→DC-DC变换器。
在运动控制领域,整流器和逆变器使用非常广泛。前面文章说了整流器感兴趣的参见J Pan:如何理解整流器,今天,我们着重看看逆变器(inverter)。
一、单桥臂方波调制
逆变器和整流器相反,其作用是将直流电变换成交流电,先从最简单的电路说起。
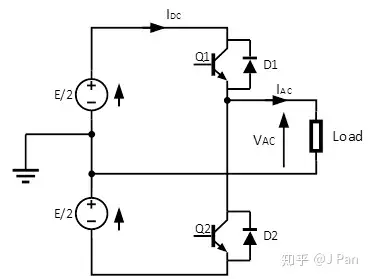
其中Q1和Q2可以为任何可控的开关型器件,通常是MOSFET或者IGBT,其工作机理和整流器中所用的晶闸管略有区别。
在上图中,显然Q1和Q2不会同时导通,否则,将出现短路。正常情况下,Q1和Q2将互补工作。现在假设Q1(含D1)工作,则根据Iac电流方向不同,有两种工作模式:
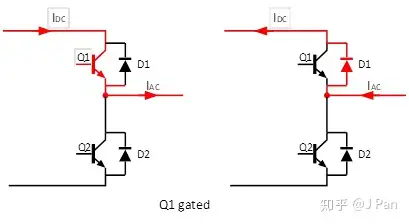
第一种工作模式为Q1工作,电流从电源端流向负载,如上图中(左)所示。第二种模式为D1工作,电流从负载流向电源,如上图中(右)所示。
同样,假设Q2(含D2)工作,则根据Iac电流方向不同,也有两种工作模式:
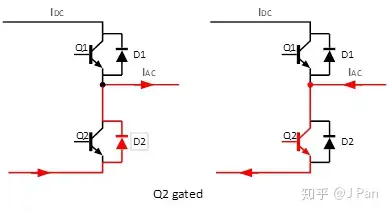
第一种工作模式为D2工作,电流从电源端流向负载,如上图中(左)所示。第二种模式为Q1工作,电流从负载流向电源,如上图中(右)所示。
将以上四种工作模式总结一下:
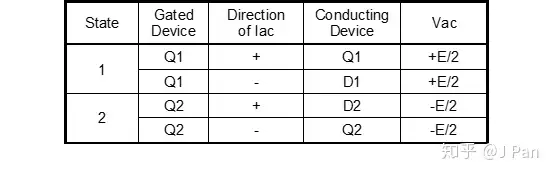
二、单相桥准方波调制
2.1 开关信号产生
前面的说的是单桥臂工作情况,虽然用的极少,但是对于了解复逆变器是很有帮助的。比如,我们再增加一个桥臂,就可以组成一个单相桥电路,如下图所示。
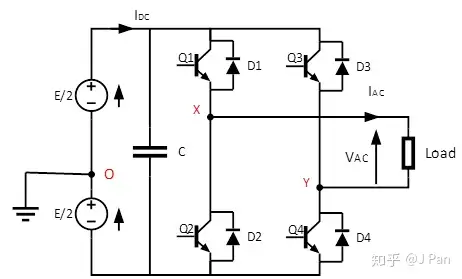
注意,与单桥臂相比,略有不同:负载的两端都连接在桥臂上,之前单桥臂的话负载有一端是连在电源上的地,这就会导致此时加到负载的电压最大可达E(前面单桥臂最大为E/2)。
现在有两组桥臂,有两种方法来确定开关信号,第一种相对比较简单,就是把四个开关管子分成两组:Q1及Q4一组,Q2和Q3一组。Q1及Q4开的时候,Q2及Q3关闭;反之,Q2及Q3开的时候,Q1及Q4关闭,示意图如下:
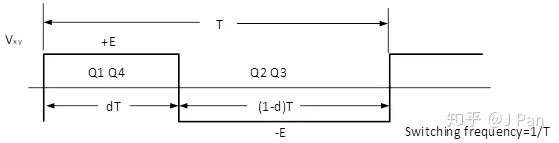
其中T为周期,d为占空比。也就是在0<t<dT时Q1,Q4开通;dT<t<T时,Q2,Q3开通。这样的话就可以得到平均电压:
Dd=Ed−E(1−d)=E(2d−1)
这样输出电压有两种:+E和-E,一般称之为双极性调制。
再来看另外一种,稍微复杂一点,基本思想就是每个桥臂都单独产生各自的开关信号。这样每组桥臂之间不必完全同步,可以有一定的相移,示意图如下:
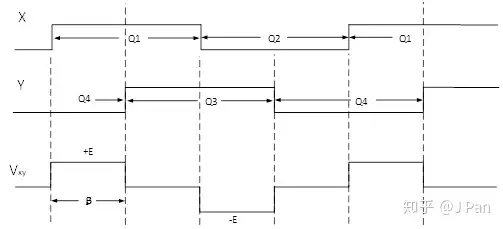
假定相移为 β ,这样加载在负载上的电压有三种:+E、-E和0。这一般称之为单极性调制。根据 不同,可以调整+E、-E和0持续时间之间的比例。
目测来看,单极性调制的基波比例更高,效果更好一些。
2.2 电压和电流分析
开关信号产生电路如下所示:
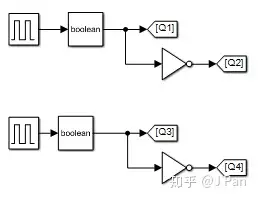
其中两个脉冲信号的频率均为50Hz,第二个脉冲的相移为120°。单相桥的仿真电路为:
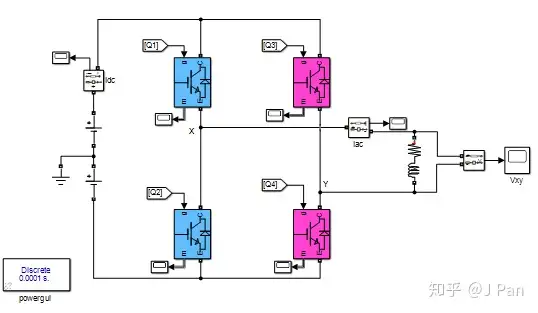
负载为: R=1Ω,L=5mH,E=200V 。
和前面分析类似,根据作用器件不同,整个电路有8中工作模式,具体如下:
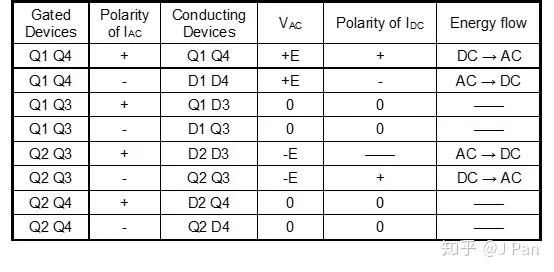
开关信号和Vxy之间关系为:
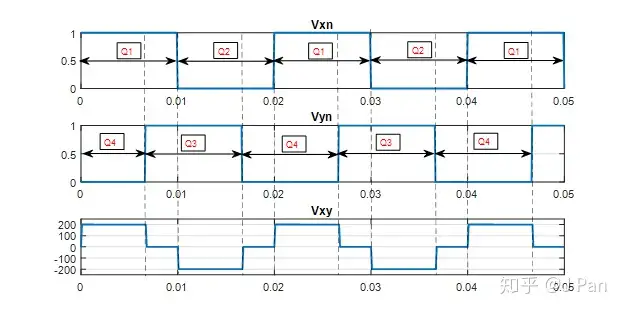
接下来分析一下整个电路的工作过程。
第一步:Q1为ON, Q4为ON,因此Q1和Q4工作,如下图所示:
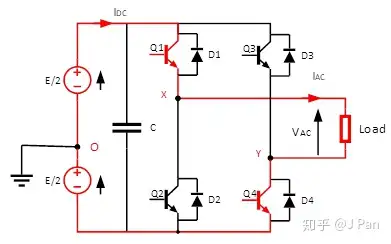
此时,Idc为正,Iac为正,并且数值都会增加,方向如图所示。
第二步:Q1为ON,Q3为ON,因此Q1和Q3导通,X和Y点电势相同,Vxy=0。由于Iac此时为正,假设负载里面有电感,电流不能发生突变,因此会找一个路径继续流动,续流的路径就是D3,如下图所示:
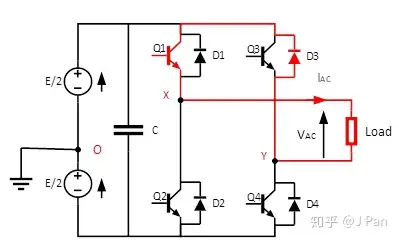
第三步:Q2为ON,Q3为ON,此时Q2、Q3导通,Q1关闭。此时,Iac此时还为正,由于之前的续流路径Q1关闭了,因此,需要有新的路径,那就是D2,如下图所示:
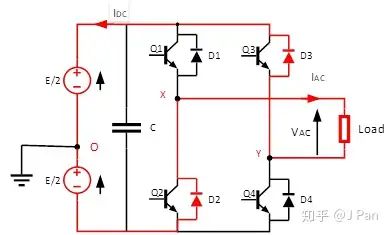
在此过程中,Iac将减小到零,电流将从负载流向电源,Idc为负,Idc数值逐渐减小到零。
第四步: Q2为ON,Q3为ON, Q2、Q3导通,有Vxo=-E/2,Vyo=+E/2,所以Iac将从零开始增加,方向为负,Idc从零开始增加,方向为正。如下图所示:
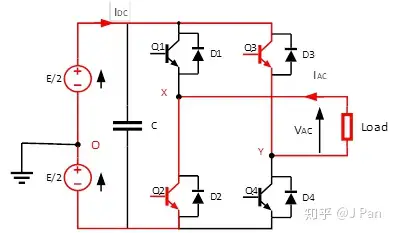
第五步: Q2为ON,Q4为ON, Q2、Q4导通,Vxy=0,Iac续流,路径为Q2、D4,具体如下:
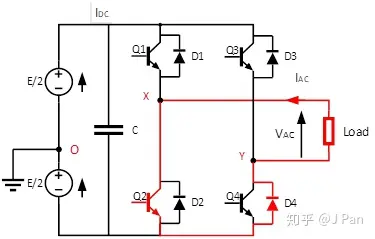
Iac(方向为负)数值减小,Idc为零。
第六步:Q1为ON,Q4为ON, Q1、Q4导通,Vxy=0,Iac续流,路径为D1、D4,具体如下:
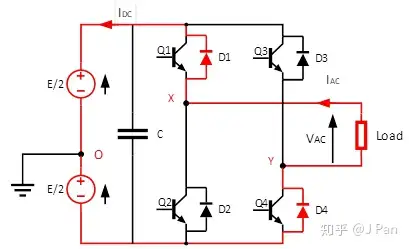
第七步:Q1为ON,Q4为ON, Q1、Q4导通,重复第一步。
有了上面的铺垫,这时来画个图就简单多了,比如Vxy和Iac的变化情况如下:
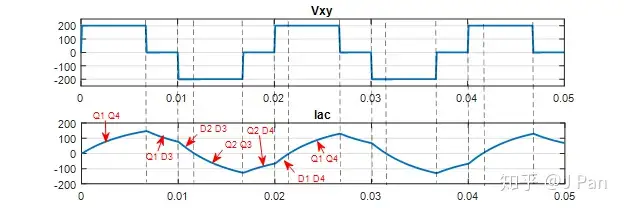
Vxy、Iac以及Idc的变化情况如下:
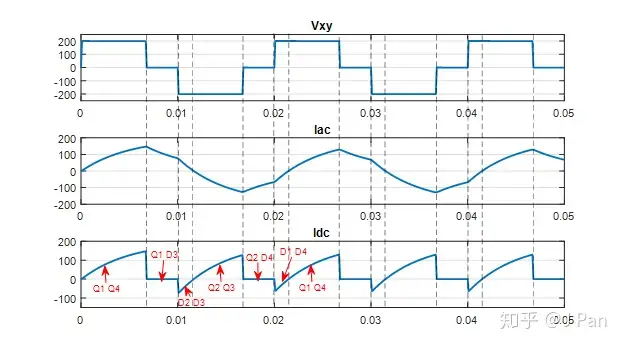
2.3 谐波分析
Simulink的POWERGUI模块提供了一个FFT分析的工具,可以计算各个谐波的比例,界面如下,其中上半部分为待分析信号,下半部分为FFT分析结果。
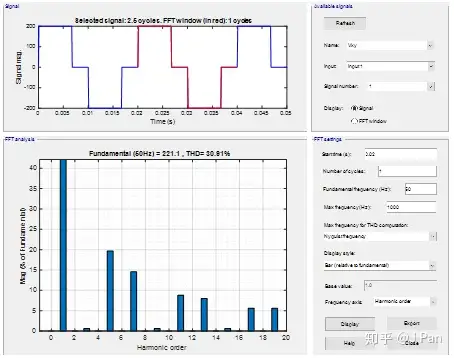
先来看一下Vxy的谐波情况,由于Vxy为准方波偶对称波形,因此可分解成为所有奇数次谐波,具体如下图:
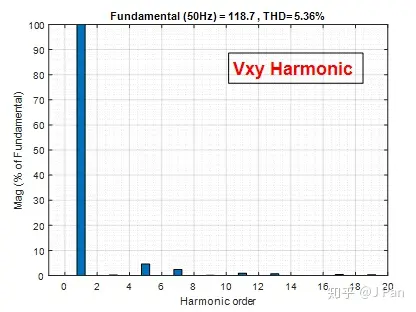
可见,其基波所占比最大,其次为5次谐波。
再来看一下负载端的波形,也为近似对称波形,因此可分解成为所有奇数次谐波(含微弱直流分量),具体如下图:
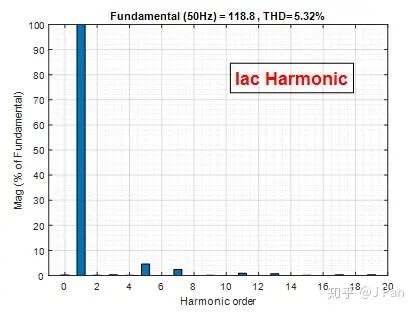
接下来再看一下直流端和交流端谐波分量的关系。下图为逆变器能量转换示意图,输入端为直流,输出为交流。
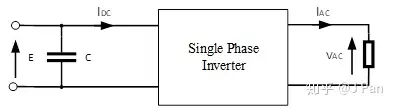
假定逆变过程中没有能量损失,则由能量守恒:
E(t)IDC(t)=VAC(t)IAC(t)
进而可以得到:
IDC(t)=VAC(t)IAC(t)E(t)
一般可以认为直流端的电压是相对比较稳定的,可以假定E(t)为横值,所以 IDC 的谐波分布就和VAC(t)IAC(t)一致。
如果假定:
VAC(t)=∑N=1∞VNsin(Nωt+ϕN)
IAC(t)=∑M=1∞IMsin(Mωt+φM)
可以得到:
IDC(t)=∑N=1∞∑M=1∞VNIMEsin(Nωt+ϕN)sin(Mωt+φM)
整理一下,可以得到:
IDC(t)=∑(cos[(N−M)ωt−...]−cos[(N+M)ωt+...])
上式表明,每个交流端的电压谐波与每个交流端的电流谐波相互作用,在直流端产生两个分量:谐波次数分别为N+M和N-M。直流端电流的谐波分布如下图所示:
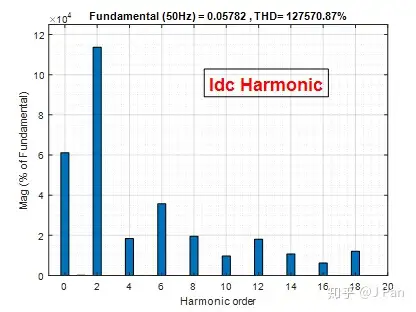
三、 单相桥脉宽调制
前面我们已经看到了,准方波调制的方法实现简单,通过H桥很容易将直流电压变换成想要的交流电压。
然而,缺点也显而易见,那就是逆变后交流端谐波分量很大。通常情况下,我们期望得到具有良好正弦性的波形,特别是对于交流电机控制,最好是理想的正弦波,因为基波之外的谐波不产生有效力矩,而是带来力矩的波动。
目前最常用的方法就是脉宽调制(Pulse-Width Modulation),简称PWM,其基本原理如下:
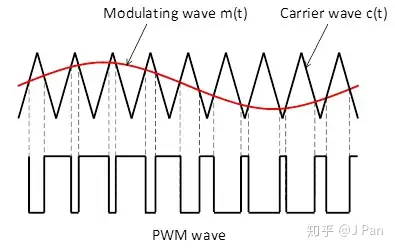
PWM由两个信号产生,一个为调制波(Modulating wave),另一个为载波(Carrier wave)。调制波的波形为我们期望得到的波形(幅值),比如正弦波;载波通常为锯齿波或三角波,频率很高,通过调制波和载波的数值比较,就可以得到PWM波,示意图如下:
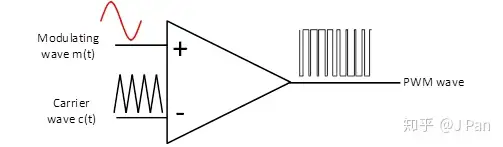
假定调制波频率为fm,峰值为 pm,载波频率为fc,峰值为pc,需要明确以下几个术语:
频率比: FR=fcfm
调制深度: MD=pmpc
前面说了,准方波调制时有单极性调制和双极性调制之分,PWM也一样。我们现在就来具体研究一下看看这两者在PWM调制方面各有何特点。
3.1 双极性调制
首先来看双极性调制,用一个比较器就可以实现4路PWM的生成,示意图如下:
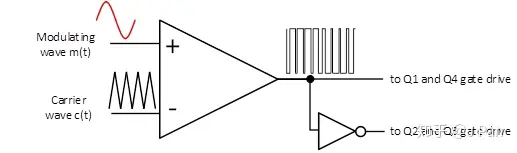
翻译成数学语言就是: Q1=Q4=Q2¯=Q3¯
假设 E=400V,fm=60Hz,fc=1080Hz,MD=0.8,R=1Ω,L=5mH ,来看一下具体的波形:
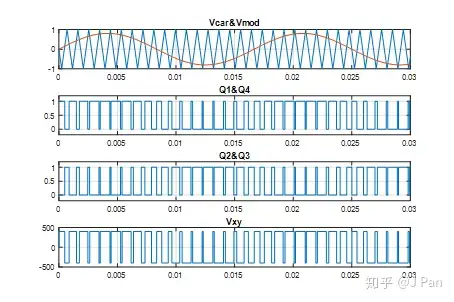
可见,产生的负载电压Vxy只有E和-E两种情况,这也就是为啥叫双极性的原因。调制波是正弦波形,也就说我们期望的Vxy也是正弦波形。实际从上图可以看出,Vxy为PWM波形,这和我们期望的正弦波形有多大差别呢?——同样,我们也做个FFT分析一下,如下:
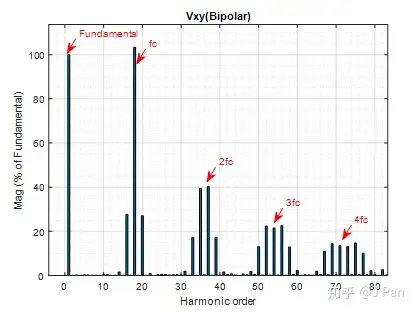
上图显示,除了基波(Fundamental wave)之外,在1、2、3、4等整数倍载波频率fc附近也出现了大量的谐波。因此,采用PWM,负载电压会出现多次谐波。
再来看看负载端电流Iac和电源端电流Idc的变化情况,如下图:
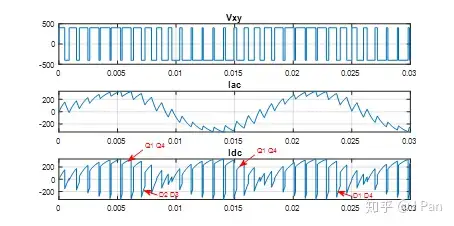
可见,在交流端,由于是RL型负载,相当于一个低通滤波器,所以Iac呈现“正弦”形貌,情况比Vxy略好,FFT分析如下:
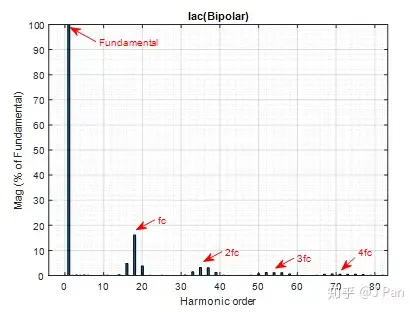
谐波组成和Vxy类似,但是高次谐波(1、2、3、4等整数倍载波频率fc附近)的幅值有较大程度的衰减,基波被较好的保留。对于直流端的电流,前面分析了,取决于Vxy谐波分量和Iac谐波分量,因此谐波最丰富,FFT分析如下:
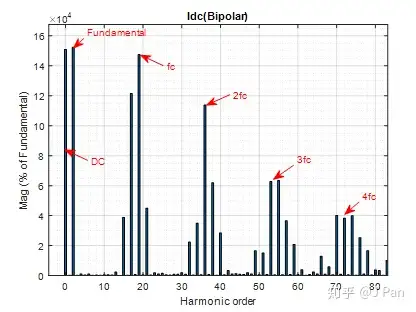
3.2 单极性调制
双极性调制只需要一个比较器就行,简单易实现,单极性调制则需要两个比较器,如下图所示:
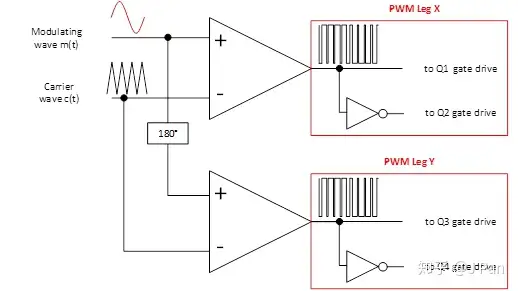
也就是说每个桥臂的管子都有独立的控制信号:第一个比较器产生Q1、Q2的门驱动信号,第二个比较器产生Q3、Q4的门驱动信号。至于为啥两个两个调制波之间的相位差为180°,请看之前说过的电路图:
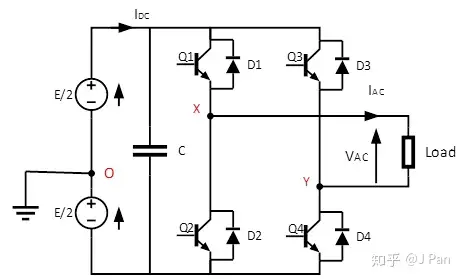
Q1、Q2控制的是Vxo,Q3、Q4控制的是Vyo,而我们想要的是Vxy,即上图中的Vac,显然,当Vxo和Vyo相差180时,Vxy峰值能到达最大。下图展示了调制波信号、载波信号、Q1、Q2、Q3、Q4已经Vxy的波形。
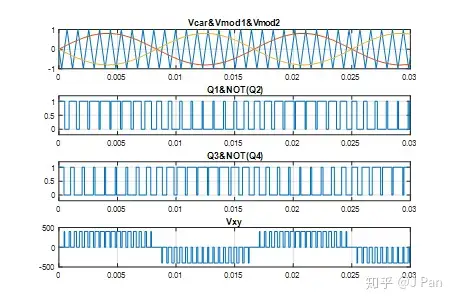
可见Vxy有三种取值:E、-E以及0,且只能在E和0或-E和0之间变化,因此称之为单极性调制。我们对最关心的Vxy近FFT分析,看看谐波分布情况:
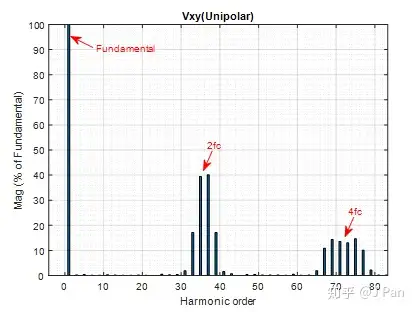
总的来说,除了基波之外,在2fc、4fc,…等附近还有其他谐波。但是很明显,。与双极性调制相比,fc、3fc,…等附近的谐波基本消失,且基波所占比例明显增加,因此,我们可以说单极性调制的效果更好一些。再来看看电流的波形:
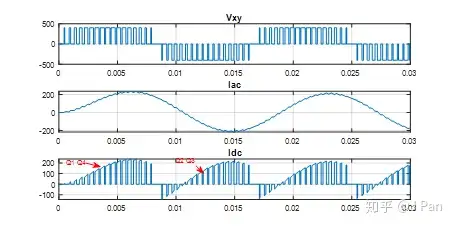
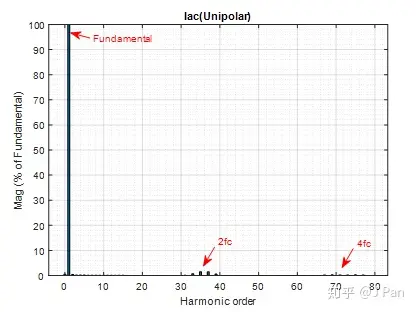
对于负载中的电流Iac,目测正弦性已经比较好,FFT分析如下,可见基波占绝对比例,其余只有2fc、4fc,…等附近还有其他谐波,但比例非常小。
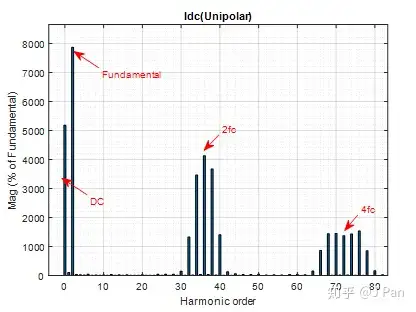
对于电源端的电流Idc,根据前面分析,由Vxy谐波和Iac谐波决定,会更丰富一些,FFT分析如下:
四、三相桥脉宽调制(SPWM)
前面介绍了单相桥的脉宽调制,实际上工程中使用最多还是三相桥,其基本电路图如下:
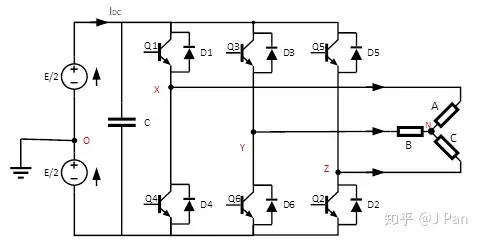
有三个桥臂(Leg)组成,每个桥臂含上下两个管子,Q1、Q3、Q5为三个上桥臂管,Q4、Q6、Q2为三个下桥臂管。每个桥臂中点都连接到负载端的每一相。
根据前面的分析,每个桥臂单独调制谐波更少,因此,对于三相负载而言,多采用单极性调制,示意图如下:
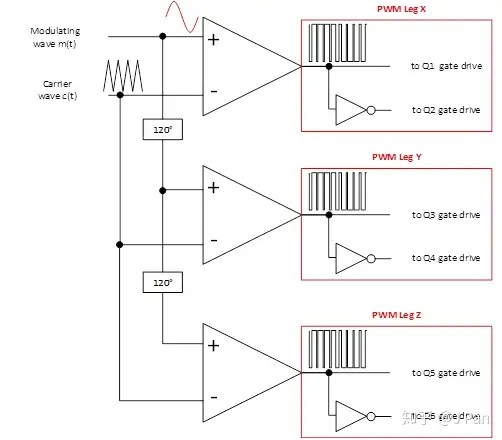
假如我们想要产生三相各差120°的三相交流电压,可采用的调制波、载波以及6个管子的开关信号如下:
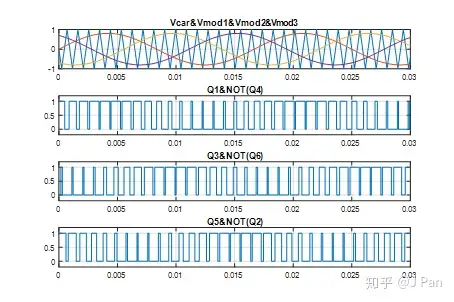
接下来再来分析一下调制出的电压情况。从前面的电路图可以看出,Q1导通的时候,Vxo(Vao)=E/2;Q4导通的时候,Vxo(Vao)=-E/2;因此可以通过Q1至Q6的开关信号确定Vao、Vbo、Vco的电压,其取值为E/2或-E/2,为2 level,具体如下图所示:
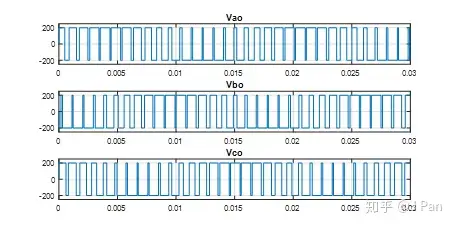
可通过Vab=Vao-Vbo来计算线电压Vab,用类似的公式可计算其他两组线电压Vbc和Vca,如下图所示:
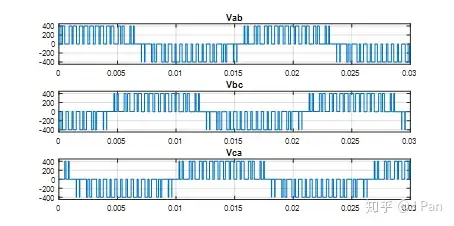
可见线电压为3 level,即取值可以为E,0或-E。
现在再来看一下相电压。我们知道,相电压为绕组端部相对于中性点N的电压,而我们已经知道绕组端部相对于电源接地点O的电压,我们把两者建立联系如下:
{Vao=Van+VnoVbo=Vbn+VnoVbo=Vcn+Vno
其中Vno为绕组中性点N到电源接地点O的电势差。若三相负载为对称负载,由基尔霍夫电流定律,有:
iA+iB+iC=0
所以可以得到:
Van+Vbn+Vcn=0
所以有:
Vao+Vbo+Vco=Van+Vbn+Vcn⏟0+3Vno
可以得到:
Vno=Vao+Vbo+Vco3
这样相电压
{Van=Vao−VnoVbn=Vbo−VnoVbn=Vco−Vno
三相绕组的相电压波形如下图所示,为5 Level。
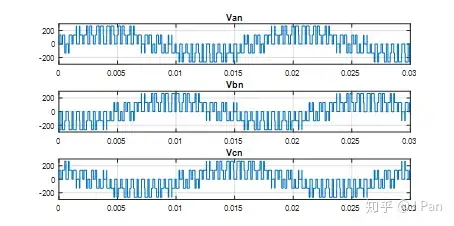
三相绕组的相电流压波形如下图所示,经过负载的低通滤波,电流已经基本接近于正弦。
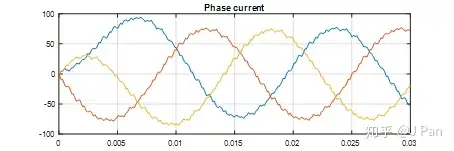
电源端的电流如下:
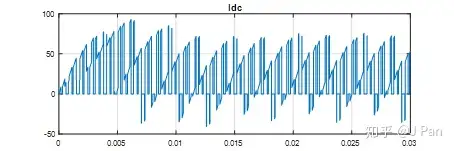
采用正弦波作为调制波进行脉宽调制的方法称之为SPWM,即Sinusoidal Pulse Width Modulation。
五、三相空间矢量调制(SVPWM)
除了SPWM,我们还经常听说SVPWM(Space Vector Pulse Width Modulation),这又是什么意思呢?——其实本质并无太大区别,就是调制波不同而已,具体来说,SVPWM采用的调制波不是正弦波,而是马鞍形波——一次正弦和三次正弦的叠加,示意图如下:
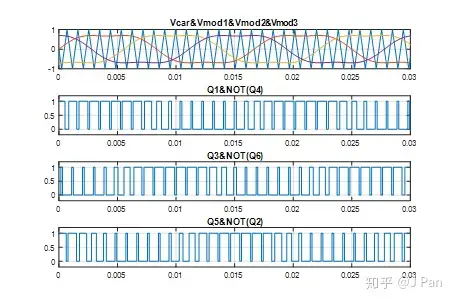
这样就可以得到三相绕组对于电源接地点的电压波形为(滤波后):
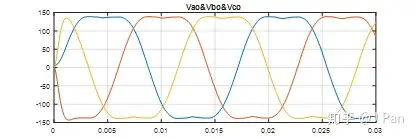
也呈现马鞍形,这貌似和我们想要的正弦波形不一致啊——不要着急,我们继续分析。假设马鞍形的数学表达式为:
s=Asin(wt)+Bsin(3wt)
三相绕组相对于电源接地点的电压为:
{Vao=Asin(wt)+Bsin(3wt)Vbo=Asin(wt+120°)+Bsin(3(wt+120°))Vco=Asin(wt−120°)+Bsin(3(wt−120°))
这样,相电压
{Van=Vao−Vno=Asin(wt)Vbn=Vbo−Vno=Asin(wt+120°)Vcn=Vco−Vno=Asin(wt−120°)
可见Vao,Vbo,Vco引入三次谐波不会引起三相绕组相电压Van,Vbn,Vcn的三次谐波,对相电压并无影响,线电压波形(滤波后)如下:
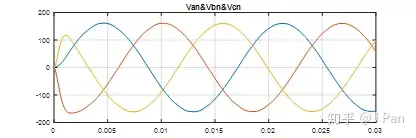
当然,对线电压也没影响,波形(滤波后)如下:
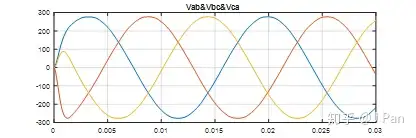
可能会有童鞋有疑问,既然没影响,我们费劲巴拉加入个三次谐波干嘛?——对波形形状没影响,但是对最大能达到的幅值有影响啊,请看下图:
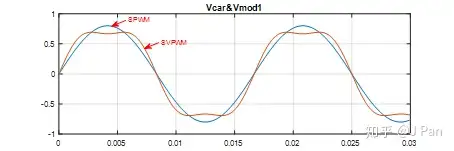
上图中有两条曲线,其中正弦的数学表达式为:
sine=0.8⋅sin(2π⋅50⋅t)
马鞍形的数学表达式为:
saddle=0.8⋅sin(2π⋅50⋅t)⏟fundamental+16⋅0.8⋅sin[3⋅(2π⋅50⋅t)]⏟third
显然,正弦波的最大值是0.8,马鞍形的最大值复杂一些,不过不是重点,我们直接给结论: 0.8⋅3/2。这是啥意识呢?——对于同样的基波(幅值0.8),马鞍形的调制波的最大值只有正弦波的3/2。
换句话说,当载波的最大幅值为1,调制深度 MD=1 的时候,马鞍形的最大值也应该是1,而此时,马鞍形的基波则可以达到2/3≃1.15 。此时若采用正弦波调制,则基波最大只能达到1,具体见下图:
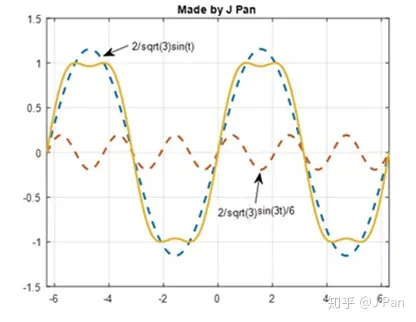
马鞍形波调制对直流电源的利用率更高,这也是为啥在交流电机控制中SVPWM广泛使的原因。相对SVPWM有更深入了解,可阅读J Pan:如何深入理解SVPWM?
部分Simulink模型(R2019A):
